log(�ΐ�)�Ƃ͉��Ȃ̂��y���o�ŃJ���^���ɍ��Z���w�z

�ΐ��̈Ӗ���v�Z���S���킩��Ȃ��I
log���ĉ��H
���Z���ɂ悭����Ȏ��������܂����A�����ƈӖ������킩���Ă���ƂĂ��ȒP�ȒP���ł��B
��{���班�����������āA�}�X�^�[���Ă��܂��܂��傤�B
�܂�log���ĉ��H
log�̂�������Ƃ������
log�̌v�Z��������l����O�ɁA�܂�log����̉����Ӗ����Ă���̂��𗝉����邱�Ƃ�����ł��B
log�̈Ӗ�
���̎������Ă��������B

(1)��(2))�̓����͊ȒP�ł���ˁB
x=2,y=3�ł��B
�����A(3)��z�͂ǂ��ł��傤�B
����ɓ��Ă͂܂�悤�Ȑ��͎v�����܂�����ˁB
�����A���̂悤�Ȑ��͕K�����݂����̂ł��B
����z���L���ŕ\�����̂��A�ΐ��ł��B

���̂Ƃ� z=log[2]6�Ə����܂��B([]�̒��̐����͏����������܂�)
�܂�Alog[2]6�́A2�����悷���6�ɂȂ�̂����w�����ł��B
�v�Z�ł���log
log�Ə����Ă��Ă��A���ʂ̐��Ƃ��đ��݂�����̂�����܂��B
�Ⴆ�A��قǂ̎���x=log[2]4=2�ł����Ay=log[2]8=3�Ƃ����������ł��B
�Q����ɂ��āA������log�ɂ��čl���Ă݂܂��傤�B
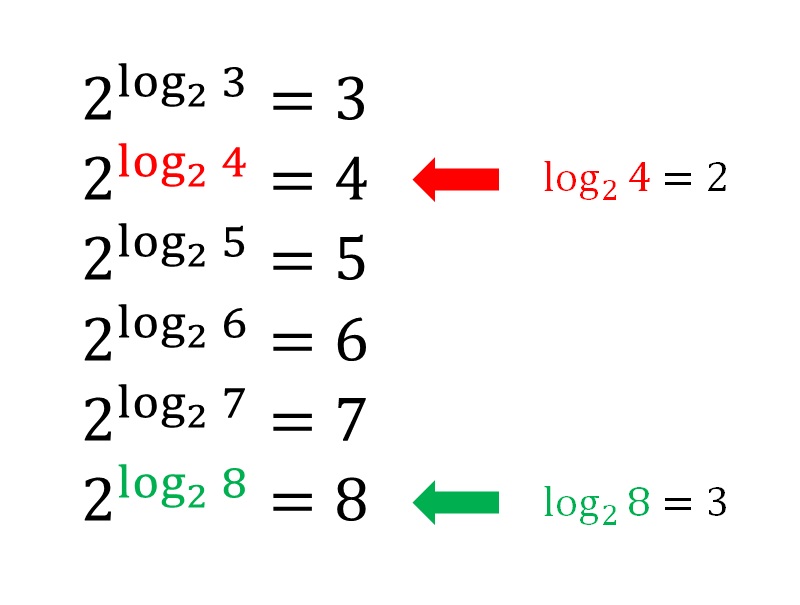
�Q�����悵�Ă��A�R�ɂ͕��ʂȂ�܂���B
�Ȃ̂ŁA���������Ƃ��ɂ�log���g���K�v������܂��B
�������A�Q�����悵�āA�S��W�ɂ��邱�Ƃ͂ł��܂���ˁB
����������log�ɂ��ẮA�l�����߂邱�Ƃ��ł��܂��B
��̋L���̈Ӗ����K�����Ƃ��ɁA��̂܂܂ŗǂ����̂ƁA������ƌv�Z�ł�����̂�����܂�����ˁB
����Ɠ����ŁAlog�̂܂܂ŗǂ����̂ƁA������ƌv�Z�ł�����̂�����܂��B
�ȏオlog(�ΐ�)�̊�{�A�Ƃ������ƂɂȂ�܂��B
�X�|���T�[�h�����N
�ΐ���3�̌v�Z�@��
log�̌v�Z�������ł́A3�̌v�Z�@��������܂��B
�����͑S�āA�w���̌v�Z�@�����瓱������̂ł��B
�����w���̌v�Z�@���������炢���܂��傤�B
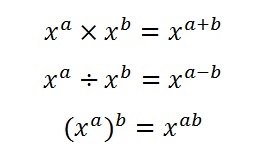
�|���Z����ƁA�w���ł͑����Z�B
����Z����ƁA�w���ł͈����Z�B
�ׂ���̌v�Z������ƁA�w���ł͊|���Z�A�Ƃ����@���ł����B
�����O��ɁA�ΐ��̌v�Z�@�����Љ�܂��B
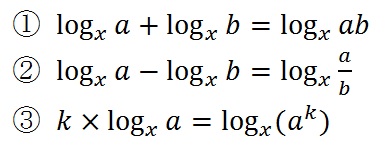
�ۈËL���Ďg����悤�ɂ��܂��傤�B
�����ËL�����ȕ��́A�@���珇�Ԃɋ�̓I�Ɍv�Z���čl���Č��܂��傤�B
(�������牺�͓���Ɗ������疳�����Ă����v�ł�)
���ꂼ��̎��̌v�Z���ʂ����Ă݂�ƁA����̌v�Z�@���̒ʂ�ɂȂ��Ă��邱�Ƃ��킩��܂��B
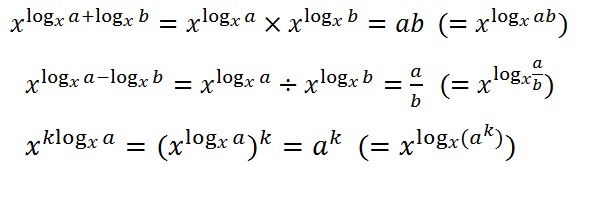
log�̂܂Ƃ�
log�̈Ӗ��͗����ł��܂������H
�o���Ȃ��Ƃ����Ȃ��̂́Alog�̈Ӗ��ƁA�v�Z�@���ł��B
������x���K���āA�}�X�^�[���Ă��܂��܂��傤�I