微分とは何なのか【感覚でカンタンに高校数学】

「微分って何？」

「何か名前が難しそう」

「結局何の計算してるのかわからない」

数学が苦手な人の中には、数Ⅱの「微分」は名前だけでも拒否反応が出てしまう人もいます。

しかし、実は「微分」は高校数学の中ではめちゃくちゃ点を取りやすい単元の一つです。

微分の計算の意味を理解して、一気に得意分野にしてしまえるよう、カンタンに解説します。

微分って結局何をしている？

微分＝接線の傾きを求める計算

まずはじめに、一番大切なことを言っておきますね。

微分は、接線の傾きを求めるための計算です。

学校の授業の微分では、計算方法ばかり教えられて、「計算はできるけど、結局何をしているのかわからない」という人が出てくることがあります。

「何をしているのか分からない」というのは数学では致命的なので、絶対に押さえておいてほしいポイントです。

今から説明することはすべて、接線の傾きを求めるための話です。

微分とは…接線の傾きを求めるための計算

直線の傾き

接線の話に入る前に、まず普通の直線のことを復習しておきましょう。

直線の方程式は、中学２年生で習う一次関数で登場します。

ｙ＝aｘ+b、ですね。

この式の中のaのことを、「傾き」と呼びました。

この傾きは、「変化の割合」とも習ったと思います。

傾き（変化の割合）を求めるための計算式、覚えていますか？

そう、「えっくすのぞうかりょうぶんのわいのぞうかりょう」ですね。

呪文のように覚えさせられた記憶もあるかもしれません。

実はこの公式の変形が、微分です。

ただ、わざわざ紹介しましたが、今回はこの計算は使いません。

頭の片隅にでも置いておいてください。

接線の具体例

言葉だけでは全然イメージしにくいと思うので、一つ簡単な例を出してみます。

次のグラフを見てください。

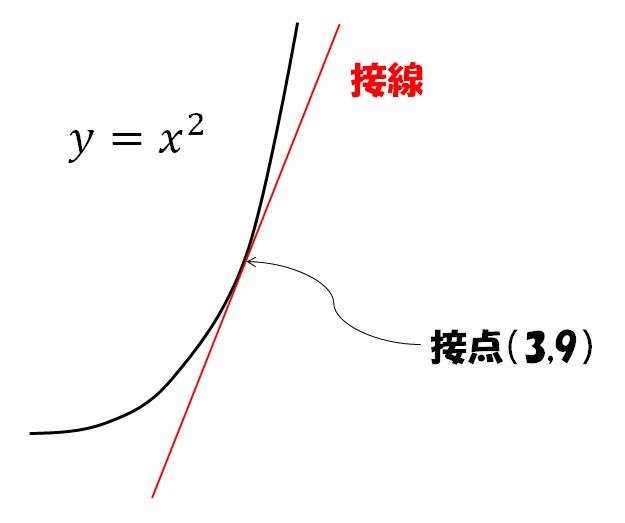
これは中学で習う放物線と直線のグラフですね。

直線は、放物線と点（3,9）で接しているのがわかると思います。

さて、この直線の方程式は、どんな式でしょう？

直線の方程式を求めるためには、やっぱり傾きの値が欲しいですよね。

これが、なんと微分で一瞬で求められてしまいます。

細かい計算は省略しますが、この直線の傾きは６とわかります。

（一応、式だけ載せておきます。計算方法は別の記事で）

というわけで、この放物線の接線は、傾きが６で、点（3,9）を通るということがわかりました。

ちなみにこの傾きのことを、微分係数といいます。

直線のｘの係数を、微分で求めるから、微分係数です。

微分係数…微分で求めた接線の傾きの値

微分のイメージ

微分とは、接戦の傾きを求めることだと言いました。

これを図でイメージすると、「グラフをズーム（拡大）して、無理やり直線として考える」ということになります。

このイメージについては、他のサイトでわかりやすく解説されていたので、そちらも併せてご覧ください。

外部サイト＞＞微分とは何か？－中学生でも分かる微分のイメージ

微分の計算方法

微分の計算方法そのものは、別の記事で詳しく解説します。

この記事では、あくまでも、「微分で何をしたいのか」の全体イメージをつかんでください。

ただ、微分の計算自体はとても簡単なので、学校の授業や教科書でも理解できるかもしれません。

計算方法はこちら。

微分係数・導関数とは何なのか【感覚でカンタンに高校数学】

接線の方程式

微分を使ったら接線の傾きがわかる、と言ってきました。

しかし、傾きまで求めておいて、直線そのものの式を求めないというのも、なんだか中途半端ですよね。

実際、問題などでは「接線の方程式を求めなさい」と出題されます。

ここでは、高校数学式の、接線の方程式の求め方を解説します。

直線の公式

さきほどの接線を例に挙げてみます。

傾きが６で点（3,9）を通る直線、というところまで分かっていました。

実はここまで分かっていたら、中学生でも直線の方程式を求めることができます。

中学生風だと、ｙ＝aｘ＋ｂに傾き６と(3,9)を代入して、ｂの値を求めますね。

これでも式そのものは求めることはできますが、今後応用問題に対応できなくなってしまいます。

なので、ここで高校数学式の、直線の求め方を復習しておきましょう。

高校数学の直線の公式は、次のようになっています。

２つ形がありますが、どちらでも構いません。

オススメは上の形です。

教科書だと下の形で載っているので、覚えやすい方で覚えましょう。

これを使って、接線の公式を求めていきます。

ちなみに、勘が良い人は気づくかもしれませんが、これは数Ⅰの二次関数の公式にそっくりですね。

接線の式の求め方

さて、接線の話に戻ります。

先ほどから話題になっている接線は、傾き６で点（3,9）を通ります。

これを先ほどの公式に代入すること、こうなります。

というわけで、ずっと話題になっていた接線は、ｙ＝６ｘー９ということがわかりました。

先ほど一瞬触れましたが、微分を使って求めた接線の傾きのことを微分係数といいます。

特に、x=pのときの微分係数（傾き）をｆ’(p)と書きます。

なので、接点(p,q)を通る直線の公式は、傾きがｆ’(p)なので、

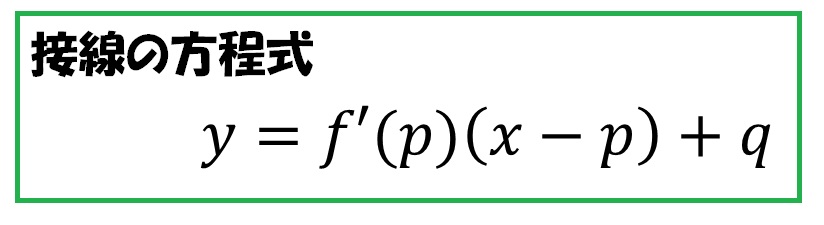
というように書けます。

ｆ’(p)…ｘ=pのときの微分係数

まとめ

微分のイメージは理解していただけましたか？

雰囲気がわかってきたら、実際の計算方法などの解説ページも読んでみてください。