�����W���E�����Ƃ͉��Ȃ̂��y���o�ŃJ���^���ɍ��Z���w�z

�u�����W�����ĉ��H�v
�u�������ĉ��H�v
����ȍ��Z�������̂��߂́A�����V���[�Ypart2�ł��B
����́A�����ɓo�ꂷ��P�ꂽ�����A�ȒP�ɉ�����܂��B
�����̕��K
�����Ƃ́H
�����̊�{�ɂ��Ă̋L���ŁA�����̈Ӗ��ƊT�v�ɂ��ĉ�����܂����B
�����Ƃ́A�u�ڐ��̌X�������߂�v�Z�v�̂��Ƃł��B
�������g���ƁA����a���{b�̎��̂����Aa�̒l�����߂邱�Ƃ��ł��܂��B
�ڐ��̕�����
�ڐ��̌X�������߂���́A�����̌������g���āA�ڐ��̎����̂��̂����߂邱�Ƃ��ł��܂��B
�����̌������g���Ƃ��́A�ʂ�_�̍��W�ƁA�X�����K�v�ł��B

�u�����W���v���ĉ��H
�����W���c�ڐ��̌X��
�܂��́A�����W���i�тԂ������j�ɂ��Ăł��B
������́A�O��̋L���ł����ɓo�ꂵ�Ă��܂��B
�����W���Ƃ́A����O���t�̐ڐ��̌X���̒l���̂��̂̂��Ƃł��B
���ɁAx=p�̂Ƃ��̐ڐ��̌X���̂��Ƃ��A���f(p)�i�G�t�E�_�b�V���E���j�Ə����܂��B
�Ⴆ�A����O���t��x=3�̂Ƃ��̔����W���́A���f(3)�i�G�t�E�_�b�V���E�R�j�ł��B
�ڐ��̕����������߂邽�߂ɂ́A�܂������W�������߂�̂��挈�ł��B
�����̌����ɂ́A�X�����ǂ����Ă��K�v������ł��ˁB
�����W���̋��ߕ�
�����W�������߂邽�߂ɂ́A�������v�Z���K�v�ł��B
�����A���̌v�Z�A���U�@�ł�낤�Ƃ���Ƃ߂��Ⴍ����ʓ|�ł��B
��`�ʂ�ɋ��߂悤�Ƃ���ƁA���f(p)�͎��̂悤�Ȍv�Z������K�v������܂��B
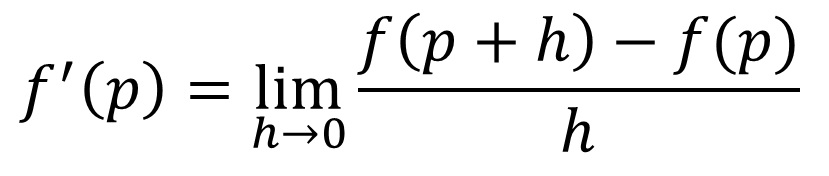
���ꂪ�{���̔����̒�`���ł��B
�҂��Ă��������A���߂�̂͂܂������ł��B
�u�L���̈Ӗ�����킩��Ȃ��I�v�Ƃ����l���قƂ�ǂł��傤�B
����lim�i���~�b�g�j�̌v�Z�́A�ڂ����͐��V�́u�Ɍ��v�Ƃ����P���ŏK�����e�ł��B
�u���������A�K�`���n���������Ȃ�����Ȃ����c�v�Ƃ������ƂɂȂ��Ă��܂��܂���ˁB
����Ȍv�Z����Ă��܂���B
���S�����������B
���ۂɂ́A���̌v�Z�����Ȃ��Ă������悤�ɁA���������g���Čv�Z�����܂��B
���̔��������A�u�����v�ł��B
�X�|���T�[�h�����N
�u�����v���ĉ��H
�����c�����W�������߂邽�߂̌v�Z��
����A��`�̎��ǂ���ɔ����W�������߂�̂́A���ɑ�ςł��B
�Ȃ̂Ŏ��ۂɂ́A�����W���������ƊȒP�ɋ��߂���@���g���܂��B
���ꂪ�A�����i�ǂ������j�ł��B
�����́A�����W�����J���^���ɋ��߂邽�߂̌v�Z���ł��B
�����̋�̗�
�����̌v�Z���@�́A��قǂ��Ƃ��āA��̓I�ȓ������Љ�܂��B
��Ƃ��āA�������̐ڐ��̌X�������߂Ă݂܂��傤�B
���̕������̎�����A����v�Z������ƁA���������߂邱�Ƃ��ł��܂��B
���̓��������߂��Ƃ̂��Ƃ��A�u��������v�Ƃ����܂��B
�������ďo�Ă��������ɁA�ړ_�̂����W��������ƁA�����W�������܂�܂��B
�Ⴆ�A�����R�̂Ƃ��̔����W�����f(3)�����߂�Ƃ��́A���̂悤�Ȍv�Z�ɂȂ�܂��B

�����̌v�Z�i�P�j
���̊����瓱�������߂�A�ڐ��̌X���i�����W���j�������ɂ킩��悤�ɂȂ�܂��B
���̊̐S�̓����́A���͂ƂĂ��ȒP�Ȍv�Z�ŏo�����Ƃ��ł��܂��B
��������������̂ŁA�ǂ�ȃ��[���ɂȂ��Ă��邩�l���Ă݂Ă��������B
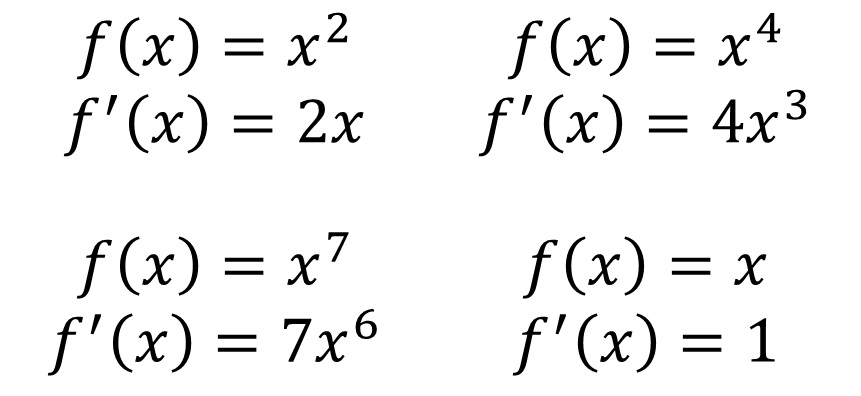
���������ɂ킩�����Ǝv���܂����A���̎w���i�Z��̕����̐����j��O�Ɋ|���Z���āA�w�����P���������邾���ł��B
���X�P��̂Ƃ��́A���������ČW�������ɂȂ�܂��B
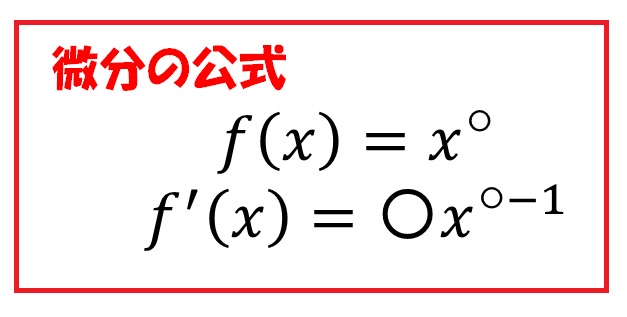
���ꂽ��Q�b�Ōv�Z�ł���悤�ɂȂ�܂��B
�����̌v�Z�i�Q�j
�X�Ɏ��̗�𗝉�������A�����̌v�Z�̓}�X�^�[�����ƌ����Ă������ł��B
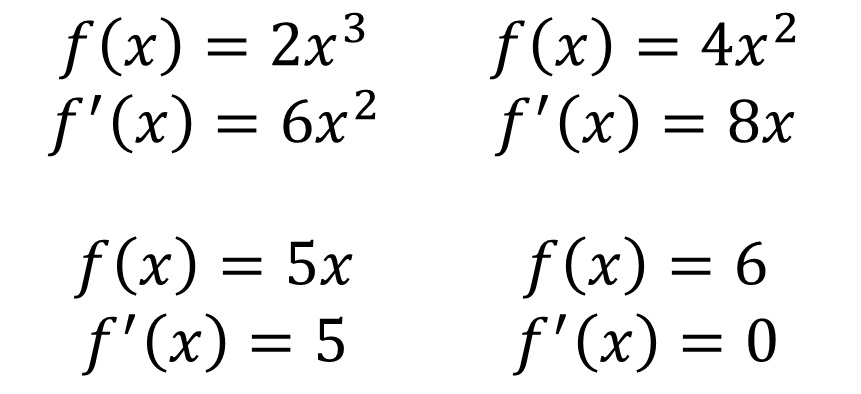
���̑O�ɌW�����t���Ă��Ă��A�Ƃɂ��������悤�Ɏw����O�Ɋ|���Z���܂��B
�܂��A�萔���i�����̐��j�͔�������ƂO�ɂȂ��ď����Ă��܂��܂��B
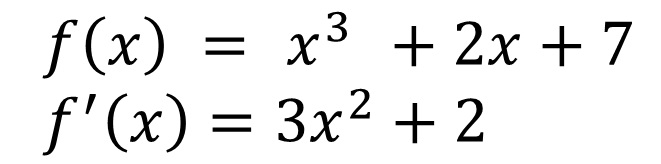
�X�ɁA���̎����{��[���܂ޑ������ł��A���ꂼ��̃p�[�c���ƂɌv�Z���đ��v�ł��B
���K���
���ۂɐڐ��̕����������߂�v�Z���A�ŏ�����Ō�܂ł���Ă݂܂��B
���̗��ɂ��āA�l���Ă݂܂��傤�B
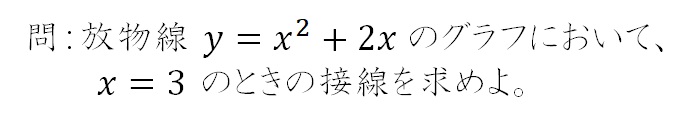
�ǂ������������邩�A�����ł��l���Ȃ���ǂݐi�߂Ă��������ˁB
�������牺�ɃX�N���[������Ɠ������o�Ă��܂��B

���ꂾ���̍�Ƃ��A�p�b�Ǝv�����Ăł���悤�ɂȂ邱�Ƃ��ŏ��̖ڕW�ł��B
�܂Ƃ�
�Ō�ɂ��̋L���̓��e���܂Ƃ߂Ă����܂��B
�����F�����W�������߂邽�߂̎�
�����F���Ƃ̊����瓱�������߂�v�Z
�������������āA���ӒP���ɂ��Ă��܂��܂��傤�I