��f(x)�Ƃ͉��Ȃ̂��y���o�ŃJ���^���ɍ��Z���w�z

f(x)���ĉ��H
y=�����ƁA��(x)=�������Ⴂ�́H
�m�ł悭���Z��N���ɕ�����鎿��ł��B
����́A��f(x)���J���^���ɉ�����Ă����܂��B
��{���̊�{���班�����������Ă����܂��傤�B
�܂����Ƃ͂ȂH
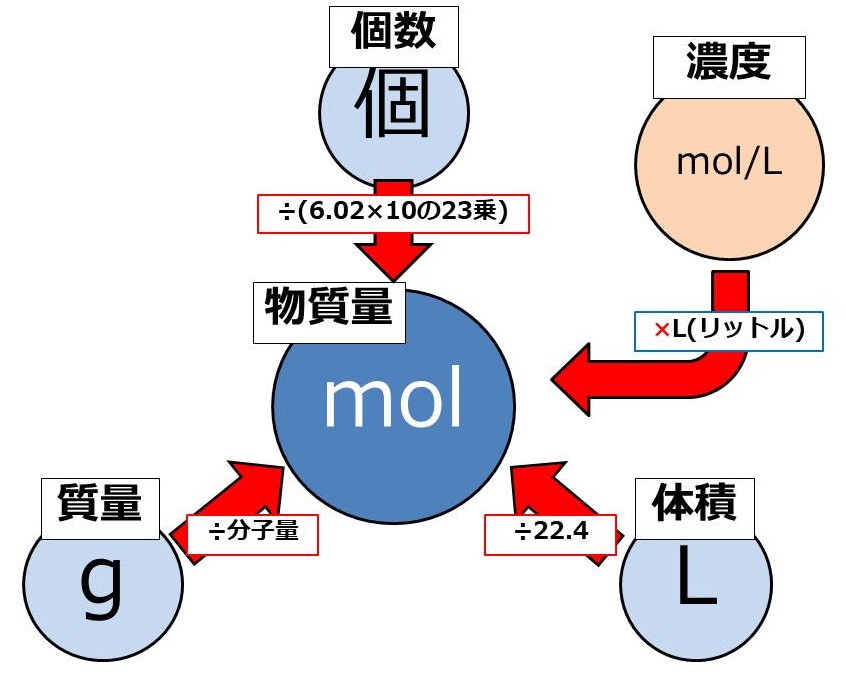
���́A���z�̏d�v�Z�c�[����
��(x)�𗝉����邽�߂ɂ́A�u���v���ǂ��������̂Ȃ̂��A���o������ł����K�v������܂��B
�Ⴆ�ł����Aweb���A�v���ŁA�g�����痝�z�̏d���v�Z���Ă������̂�����܂���ˁB
����͂܂��Ɋ��̓T�^�I�ȗ�ł��B
���Ƃ��u����l(x)����A�����ʂ̒l(y)�����߂�c�[���v�ł��B
���z�̏d�v�Z�c�[���́A�g���Ƃ����l(x)����A���z�̏d(y)�Ƃ����l���v�Z���Ă���܂��B
���Ƃ��ΐg��160cm�����z�̏d51.2kg�A170cm��57.8kg�Ƃ�������ł��B
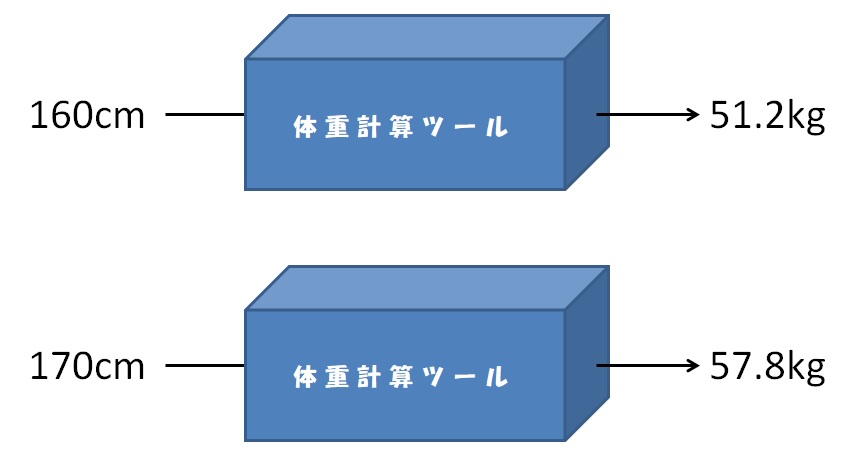
���ꂪ���̃C���[�W�ł��B
�ȒP�ł���ˁB
����()�̈Ӗ��Ƃ�
��قǂ̑̏d�v�Z�c�[���Ƃ������ɁA���Ƃ������O��t�����Ƃ��܂��傤�B
���̂Ƃ��A�����g���ċ��߂��������A��(���Ƃ̐�)�Ə����܂��B
�Ⴆ�A�g��160cm�̗��z�̏d��51.2kg�Ȃ̂ŁA��(160)=51.2�A�ƂȂ�܂��B
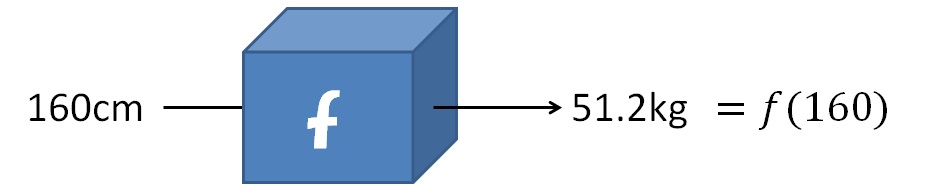
�����悤�ɁA��(170)=57.8�Ə����܂��ˁB
��������ď����ƁA�g����cm�̐l�̗��z�̏d�̂��ƂȂ̂��A��ڂŕ�����悤�ɂȂ�܂��B
��(150)=45�Ə����Ă�����A�g��150cm�̗��z�̏d��45kg���A�Ƃ����Ӗ��ł��B
���z�̏d�̌v�Z���́H
���āA�����܂Őg�����痝�z�̏d���v�Z���Ă݂܂������A�̐S�̌v�Z���@�������Ă��܂���ł����B
�������̂������ƁA157cm��A168cm�̐l�̗��z�̏d��������܂���ˁB
���͂������̗��z�̏d�́A�g����x�Ƃ����A���̂悤�Ȏ��Ōv�Z���Ă��܂����B
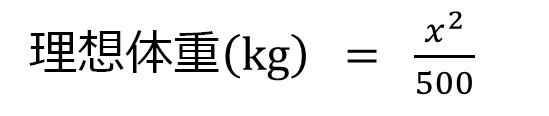
��قǂ̌v�Z�c�[���ɂ͂��Ƃ������O��t���Ă��܂����B
���̂��ɁA����x�Ƃ���������������ƁA��̎������̂܂o�Ă���͂��ł���ˁB
�Ȃ̂ŁA��(x)�͎��̂悤�ɏ����\�����Ƃ��ł��܂��B
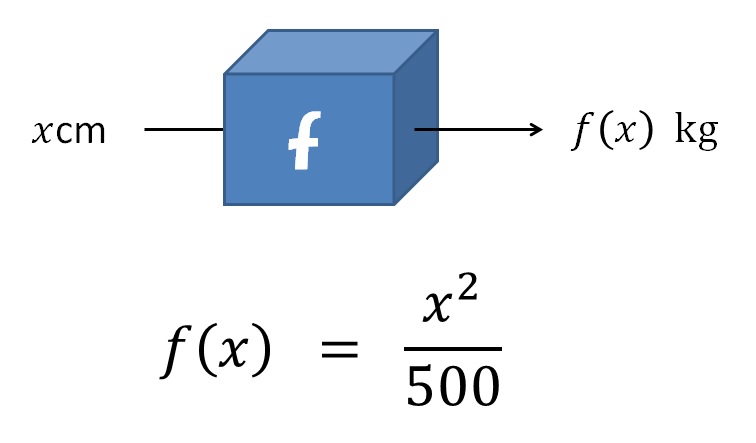
���ꂪ�܂��ɁA����(x)�̂��Ƃł��B
�u�����v�Ɓu��(x)���v�̈Ⴂ
���āA���w�܂ł͂قƂ�ǂ̊����A����(x�̎�)�Ƃ��ď����Ă��܂����ˁB
����͂���łƂĂ��g���₷���̂ł����A���̍��Z�ɂȂ��Ă킴�킴��(x)�Ȃ�Ă��̂��g���̂ł��傤���B
���Ƃ̐�����ڂł킩��
���̓����̂P�́A���͂��łɊF����킩���Ă��܂��B
��قǁA�u��������āi�����g���āj�����ƁA�g����cm�̐l�̗��z�̏d�̂��ƂȂ̂��A��ڂŕ�����悤�ɂȂ�܂��v�ƌ����܂�����ˁB
���z�̏d���������Ə����Ă��܂��ƁA����46.818�ƌ����Ă���cm�̐l�̘b�����Ă���̂��킩��Ȃ��̂ł��B
�i���Ȃ݂�153cm�Ōv�Z���܂����j
���ꂪ�A��(153)��46.818�Ə�����Ă�����A�����ɗ����ł��܂���ˁB
���������������Ă��A�킩��₷��
���ɂ��A�v�Z������������Ƃ��Ȃɂ́A��(x)�Ƃ����������͕֗��ł��B
��قǂ̗��z�̏d�́ABMI=20�Ƃ��Čv�Z���Ă��܂����B�iBMI�̐����͏Ȃ��܂��A���ׂĂ݂Ă��������j
�������ABMI=18�̂Ƃ��𗝑z�̏d�ƍl����̂ł���A�S�R�Ⴄ�v�Z���ɂȂ��Ă��܂��܂��B
���ɂ�BMI=22�ł��v�Z�������Ƃ������邩������܂���B
����ȂƂ��ɂ́A���ꂼ��̊��ɁA��,���Ƃ������̖��O��t���邱�Ƃ��ł��܂��B
����BMI=18�A����BMI=22���Ƃ���ƁA
��(160)��51.2�A��(160)��46.08�A��(160)��56.32�A�Ƃ����悤�ɏ����܂��ˁB
����l��������Α�����قǁA���͕֗�
�������Ƀo���G�[�V����������������̂ŁA����l��������Α�����قǁA��(x)�Ƃ������������֗��ɂȂ�܂��B
�t�ɁA�����l�����Ȃ��Ƃ��́A�����ŏ��������������葁���ł��ˁB
���ہA���������Ƃ��ɂ́A���Z�ł��������g�����Ƃ�����܂��B
�܂Ƃ�
���Z���w�̔����ȏ�ɂ͊����o�ꂵ�܂��B
���w�A�����M�[���������A�ڎw���i�H�Ɉ�����߂Â��Ă����܂��傤�B